判断列表是否为二叉搜索树的后序遍历

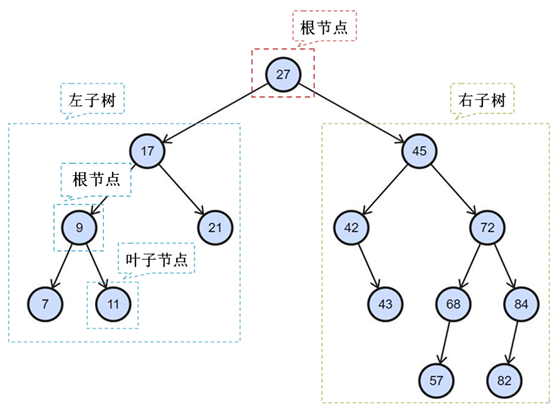
二叉搜索树（Binary Search Tree），又名二叉排序树（Binary Sort Tree），其包括3部分，即节点、左子树、右子树，而节点又可以分为根节点和叶子节点，其中，具有左子树或右子树的节点称为根节点，否则称为叶子结点，如图19-3所示。

图19-3 二叉搜索树

二叉搜索树具有以下性质：

（1）若二叉搜索树的左子树不为空，则其左子树上所有节点的值均小于或等于其根节点的值。

（2）若二叉搜索树的右子树不为空，则其右子树上所有节点的值均大于或等于其根节点的值。

（3）二叉搜索树的左、右子树也分别为二叉搜索树。

二叉搜索树的遍历分为先序、中序和后序，先序遍历的顺序为根节点→左子树→右子树；中序遍历的顺序为左子树→根节点→右子树；后序遍历的顺序为左子树→右子树→根节点。

解析代码如下：

# 资源包\Code\chapter19\1936.py
def VerifySquenceOfBST(sequence):
    # 如果是空列表直接返回False
    if len(sequence) == 0:
        return False
    # 如果是列表中只有一个元素，则必定是后序遍历
    if len(sequence) == 1:
        return True
    # 获取根节点的值
    root = sequence[-1]
    # 必须初始化边界点的值，因为该列表可能没有右子树，这样就无法使用"第一个大于根节点的方法找到左、右子树的边界点"
    border = len(sequence) - 1
    # 列表中第一个大于根节点的值，设为左、右子树的边界点
    for i in range(len(sequence) - 1):
        if sequence[i] > root:
            # 左、右子树的边界点
            border = i
            break
    # 获得边界点后，判断为False的情况
    for i in range(len(sequence) - 1):
        # 当边界点左边的值大于根节点的值，返回False
        if i < border and sequence[i] > root:
            return False
        # 当边界点右边边的值小于根节点的值，返回False
        if i > border and sequence[i] < root:
            return False
    # 当二叉搜索树没有右子树或没有左子树的情况，直接将除根节点之外组成的列表继续递归处理，否则以边界点为界限，将左子树和右子树组成的列表继续递归处理
    if border == len(sequence) - 1 or border == 0:
        return VerifySquenceOfBST(sequence[:-1])
    else:
        return (VerifySquenceOfBST(sequence[:border]) and VerifySquenceOfBST(sequence[border:len(sequence) - 1]))
# 后序遍历
print(VerifySquenceOfBST([7, 11, 9, 21, 17, 43, 42, 57, 68, 82, 84, 72, 45, 27]))
# 前序遍历
print(VerifySquenceOfBST([27, 17, 9, 7, 11, 21, 45, 42, 43, 72, 68, 57, 84, 82]))